Funktionen und Relationen: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
==== '''Funktion''' ==== | ==== '''Funktion''' ==== | ||
Eine Funktion ist eine Relation (d.h. die Zuordnung einer Zahl zu einer anderen Zahl) bei der jeder x-Wert maximal einen y-Wert besitzt. | '''Eine Funktion ist eine Relation''' (d.h. die Zuordnung einer Zahl zu einer anderen Zahl) bei der '''jeder x-Wert maximal einen y-Wert besitzt.''' | ||
Anders ausgedrückt: | Anders ausgedrückt: | ||
Jede Funktion ist eine Relation, aber nicht jede Relation eine Funktion. | '''Jede Funktion ist eine Relation, aber nicht jede Relation eine Funktion.''' | ||
==== '''Veranschaulichung''' ==== | ==== '''Veranschaulichung''' ==== | ||
| Zeile 24: | Zeile 24: | ||
Unsere '''Autos befinden sich in dem Definitionsbereich D'''. Der '''Wertebereich W beinhaltet unsere Kunden''', denen wir die Autos verkaufen (zuordnen) möchten: | Unsere '''Autos befinden sich in dem Definitionsbereich D'''. Der '''Wertebereich W beinhaltet unsere Kunden''', denen wir die Autos verkaufen (zuordnen) möchten: | ||
[[Datei:Funktion einfach.jpg | [[Datei:Funktion einfach.jpg|mini|438x438px|Vereinfachte bildliche Darstellung einer Funktion.|zentriert]] | ||
| Zeile 34: | Zeile 35: | ||
'''Das Gegenteil ist aber kein Problem''' (ein Kunde kann sich ja unter Umständen mehrere Autos kaufen). | '''Das Gegenteil ist aber kein Problem''' (ein Kunde kann sich ja unter Umständen mehrere Autos kaufen). | ||
==== '''Sonderfall''' ==== | |||
Wenn '''ein Objekt im Definitionsbereich D''' einem Objekt zugordnet ist, das '''<u>nicht</u> im Wertebereich W liegt''' ist das Ganze '''<u>weder eine Relation noch eine Funktion</u>!''' | |||
== '''Kartesisches Produkt''' == | == '''Kartesisches Produkt''' == | ||
Eine Relation ist per Definition eine Teilmenge des Kartesischen Produkts von 2 Mengen zuzüglich einer Regel, z.B. a > 2b. | Eine Relation ist per Definition eine Teilmenge des Kartesischen Produkts von 2 Mengen zuzüglich einer Regel, z.B. a > 2b. | ||
Aber was ist das kartesische Produkt eigentlich? | |||
Nehmen wir uns zu Anfang erstmal 2 Mengen (A und B): | |||
A = {x,y,z} | |||
B = {1,2,3} | |||
Das kartesische Produkt ist nun eine Menge aus diesen beiden Mengen: | |||
A x B = kartesisches Produkt ''(das vorne wird "A kreuz B" ausgesprochen)'' | |||
Diese '''neue Menge''' besteht nun jeweils aus '''Kombinationen aus den Mengen A und B''' '''<u>(quasi als würde man 2 Mengen ausmultiplizieren)</u>'''. | |||
A x B = <math> {(a,b)|a \epsilon A, b \epsilon B}</math> -> Die kleinen a und b sind irgendwelche Elemente in den Mengen A und B. | |||
Wenn man das mit unseren beiden Mengen A und B komplett macht sieht das Ergebnis grafisch ungefähr so aus: | |||
[[Datei:Kartesisches Produkt.jpg|zentriert|mini|482x482px|Das kartesische Produkt aus den Mengen A und B.]] | |||
Hierbei ist die '''Reihenfolge''' in den jeweiligen "Untermengen" '''wichtig'''. Also '''erst ein Element aus der Menge A, dann eines aus Menge B.''' | |||
Solche '''geordneten Mengen nennt man Tupel''' (vgl. tuples aus z. B. Python). | |||
Damit ist das kartesische Produkt eine Menge aus Tupeln. Es beinhaltet also praktisch alle möglichen Kombinationen aus den Mengen A und B (in dieser Reihenfolge!) | |||
==== '''Praxis''' ==== | |||
Ein praktisches Beispiel für ein kartesisches Produkt ist z. B. ein '''Skat-Spiel''': Jede Karte gibt es in 4 Variationen. Somit wären die Mengen beim Skat: | |||
'''A (Farben) = {Karo, Herz, Pik, Kreuz}''' | |||
'''B (Werte) = {7,8,9,10, Bube, Dame, König, Ass}''' | |||
Und das kartesische Produkt würde lauten: | |||
'''A x B = {(Karo,7),(Karo,8)....,(Kreuz,Ass)}''' | |||
==== '''Regeln''' ==== | |||
Als wichtige Grundregeln gelten somit: | |||
'''Erstens:''' Für die '''Anzahl der Elemente im kartesischen Produkt''' (zur Erinnerung: dafür stehen die Betragsstriche) '''gilt bei 2 endlichen Mengen:''' | |||
|A x B| = |A| * |B| | |||
'''Zweitens:''' '''Da''' das kartesische Produkt eine Kombination aus 2 Mengen ist, '''man eine leere Menge aber mit nichts kombinieren kann, gilt:''' | |||
'''A x {} = {}''' | |||
'''Drittens:''' Das kartesische Produkt ist '''nicht-kommutativ'''. Heißt im Klartext einfach nur, dass die '''Reihenfolge der Mengen und der Elemente der Tupel wichtig''' ist: | |||
<math>\text{AxB} \neq \text{BxA}</math> | |||
==== '''Praxis''' ==== | |||
Und wofür betreiben wir jetzt den ganzen Aufwand? | |||
Wenn wir eine Relation oder eine Funktion haben gibt es zusätzlich zu 2 Mengen (Definitions- und Wertebereich) ja immer noch eine Regel (z. B. a > 2b). | |||
Somit inkludiert eine Funktion oder Relation immer nur einen Teil der Tupel aus dem kartesischen Produkt (für die die Regel eben zutrifft). | |||
== '''Eigenschaften von Funktionen''' == | == '''Eigenschaften von Funktionen''' == | ||
Heißt im Klartext: Werden '''alle''' Elemente im Wertebereich W (siehe oben)... | |||
* ...'''maximal einmal''' angesprochen (heißt nicht angesprochene Elemente sind völlig okay) -> '''<u>Injektiv</u>''' | |||
* ...'''mindestens einmal''' angesprochen (die Elemente können auch ruhig öfter angesprochen werden) -> '''''<u>Surjektiv</u>''''' | |||
* ...oder '''genau einmal''' angesprochen -> '''<u>bijektiv</u>''' | |||
==== '''Injektiv''' ==== | ==== '''Injektiv''' ==== | ||
Alle Elemente in W werden maximal einmal angesprochen: | |||
[[Datei:Injektiv.jpg|ohne|mini|Injektiv.]]'''Eine Funktion ist <u>injektiv</u>, wenn:''' | |||
* Sie '''streng monoton wachsend/fallend''' ist, d.h. | |||
* die '''erste Ableitung > 0''' ist | |||
==== '''Surjektiv''' ==== | |||
Alle Elemente in W werden mindestens einmal angesprochen: | |||
[[Datei:Surjektiv.jpg|ohne|mini|Surjektiv.]]'''Eine Funktion ist <u>surjektiv</u>, wenn:''' | |||
* Man einen '''x-Wert des Intervalls in die Funktion einsetzt und der entsprechende y-Wert herauskommt''' | |||
* Die '''Funktion stetig ist''' | |||
==== '''Bijektiv''' ==== | ==== '''Bijektiv''' ==== | ||
Alle Elemente in W werden genau einmal angesprochen (surjektiv+bijektiv): | |||
[[Datei:Bijektiv.jpg|ohne|mini|Bijektiv.]]'''Eine Funktion ist bi<u>jektiv</u>, wenn:''' | |||
* Sie '''sowohl''' '''injektiv als auch surjektiv''' ist. | |||
==== '''Praxis''' ==== | |||
Wenn man die Aufgabe bekommt, eine Funktion auf diese Eigenschaften zu untersuchen sieht das meistens ungefähr so aus: | |||
'''f: [0,1] -> [0,4], f(x) = x^2''' | |||
'''Soll heißen:''' | |||
'''[0,1]''' -> Als erstes kommt der Definitionsbereich D. Bedeutet: '''Der Bereich der uns auf der x-Achse interessiert.''' | |||
'''[0,4]''' -> Dieser verweist auf den Wertebereich W. Also '''der Bereich der uns auf der y-Achse interessiert.''' | |||
'''f(x) = x^2''' -> Am Ende kommt noch die Funktion. | |||
Und wie geht man jetzt vor? | |||
Tipp: '''Funktion zeichnen!''' | |||
Dann kann man schon recht genau erkennen, ob und wie oft auf der x-Achse die y-Werte angesprochen werden. | |||
Bei Funktionen mit endlichen Bereichen sollte man zur Kontrolle aber noch die einzelnen Werte im x-Intervall in die Funktion einsetzen, um das Ganze zu überprüfen. | |||
'''Also:''' | |||
f(x) = x^2 ist eine simple Parabel. Sie ist damit auf der y-Achse nie negativ. | |||
Das interessiert uns hier aber nicht, '''wir wollen nur wissen wie sie sich auf der y-Achse von 0 bis 4 verhält.''' Und zwar nur '''im Bereich von 0 bis 1 auf der x Achse.''' | |||
Setzen wir also die '''x-Werte mal in die Funktion ein:''' | |||
'''0^2 = 0''' | |||
'''1^2 = 1''' | |||
Wir sehen: '''Die y-Werte 0 und 1 werden jeweils einmal angesprochen, die Werte 2, 3 und 4 aber nicht.''' | |||
Die Funktion ist daher '''<u>injektiv, aber nicht surjektiv.</u>''' | |||
== '''Umkehrfunktionen''' == | == '''Umkehrfunktionen''' == | ||
Siehe [[Umkehrfunktionen]]. | |||
== '''Verkettungen''' == | == '''Verkettungen''' == | ||
Die Verkettung von 2 Funktionen ist an sich ziemlich simpel: | |||
Man setzt '''in der ersten Funktion anstelle der Variablen (z. B. x) die komplette andere Funktion ein''' (wohlgemerkt für jedes x). | |||
Das wird dann "'''Verkettung der Funktion f(x) mit der Funktion g(x)'''" gesprochen und ungefähr so geschrieben: <math>f\circ(g(x) )</math> | |||
Oder auch so: '''f(g(x))''' | |||
'''Beispielrechnung:''' | |||
<math>f(x) = x^2 + x ; g(x) = 2x-1</math> | |||
<math>f(g(x)) = (2x-1)^2 + 2x-1</math> | |||
<math>= 4x^2 +1 + 2x-1</math> | |||
<math>= 4x^2 + 2x</math> | |||
Das gilt übrigens immer, egal wo die Variable steht (z. B. wenn sie als Exponent gesetzt ist). | |||
Einen Fallstrick gibt es aber! Hierzu nochmal ein Beispiel: | |||
<math>f(x) = 2x+1 ; g(x) = 3x^2-2</math> | |||
<math>g(f(2))</math> | |||
Nicht nur, dass hier die Verkettung von g mit f gesucht wird und nicht umgekehrt, es wird zusätzlich nicht mit f(x) verkettet, sondern mit f(2). | |||
Also muss man vor der Verkettung noch 2 in die Funktion f(x) einsetzen und das Ganze dann ausrechnen: | |||
<math>f(2) = 2*2+1 = 5</math> | |||
Jetzt kann es an die Verkettung gehen, indem wir das Ergebnis (5) in g(x) einsetzen: | |||
<math>g(f(2)) = 3*5^2-2 = 3*25-2 = 73</math> | |||
Done:) | |||
== '''Nachschlagewerke''' == | == '''Nachschlagewerke''' == | ||
| Zeile 60: | Zeile 215: | ||
* Injektiv, Subjektiv, Bijektiv - Daniel Jung: https://www.youtube.com/watch?v=23jng4oAwI8 | * Injektiv, Subjektiv, Bijektiv - Daniel Jung: https://www.youtube.com/watch?v=23jng4oAwI8 | ||
* Umkehrfunktionen - Daniel Jung: https://www.youtube.com/watch?v=X8QDtWIWu6Q | * Umkehrfunktionen - Daniel Jung: https://www.youtube.com/watch?v=X8QDtWIWu6Q | ||
* Umkehrfunktionen Voraussetzungen und Berechnung - MathePeter: https://www.youtube.com/watch?v=KiIcbIrmjWg | |||
* Voraussetzungen für Umkehrfunktionen - Daniel Jung: https://www.youtube.com/watch?v=tUUHFqmENvg | * Voraussetzungen für Umkehrfunktionen - Daniel Jung: https://www.youtube.com/watch?v=tUUHFqmENvg | ||
* Umkehrfunktionen: Achtung bei x quadrat - Daniel Jung: https://www.youtube.com/watch?v=AszdBZugcdo | * Umkehrfunktionen: Achtung bei x quadrat - Daniel Jung: https://www.youtube.com/watch?v=AszdBZugcdo | ||
* Injektivität beweisen - MathemaTrick: https://www.youtube.com/watch?v=9j6usdTBYbc | * Injektivität beweisen - MathemaTrick: https://www.youtube.com/watch?v=9j6usdTBYbc | ||
* Verkettung von Funktionen 1 -Daniel Jung: https://www.youtube.com/watch?v=y7MmgAdibnY | |||
* Verkettung von Funktionen 2 -Daniel Jung: https://www.youtube.com/watch?v=4pn02EvUZx0 | |||
* Verkettung von Funktionen - MathemaTrick: https://www.youtube.com/watch?v=Ln3gAhQfGzI | |||
Aktuelle Version vom 21. Oktober 2024, 19:53 Uhr
Von Funktionen und Relationen.
Allgemeines
Was ist was?
Relation
Eine Relation ist eine Regel, die einer Zahl/einem Objekt aus einer Menge einen oder mehrere Zahlen/Werte aus einer anderen Mange direkt zuordnet.
Im Regelfall spricht man bei der ersten Menge - die, deren Werte zugeordnet werden - von dem Definitionsbereich D und bei der zweiten Menge - die, deren Werte die ersten Menge zugeordnet bekommen - von dem Wertebereich W.
Funktion
Eine Funktion ist eine Relation (d.h. die Zuordnung einer Zahl zu einer anderen Zahl) bei der jeder x-Wert maximal einen y-Wert besitzt.
Anders ausgedrückt:
Jede Funktion ist eine Relation, aber nicht jede Relation eine Funktion.
Veranschaulichung
(Mir fällt jetzt ehrlicherweise kein eigenes Beispiel ein, also nehme ich eines aus einem Video)
Etwas anschaulicher ausgedrückt:
Wir nehmen mal an, dass wir ein Autohaus besitzen. Unser Ziel es damit Autos zu verkaufen.
Unsere Autos befinden sich in dem Definitionsbereich D. Der Wertebereich W beinhaltet unsere Kunden, denen wir die Autos verkaufen (zuordnen) möchten:
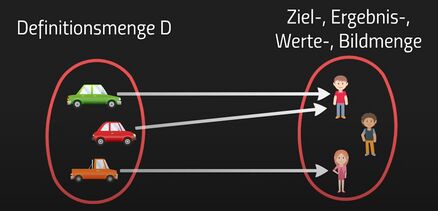
Wir sehen auf dem Bild: Das Ganze ist eine Funktion.
Begründung: Jedem Auto (x-Wert) ist genau ein Käufer (y-Wert) zugeordnet.
Es wäre keine Funktion, wenn ein x-Wert mehrere y-Werte zugeteilt bekommen hätte (man kann ein Auto ja nicht zwei Mal verkaufen).
Das Gegenteil ist aber kein Problem (ein Kunde kann sich ja unter Umständen mehrere Autos kaufen).
Sonderfall
Wenn ein Objekt im Definitionsbereich D einem Objekt zugordnet ist, das nicht im Wertebereich W liegt ist das Ganze weder eine Relation noch eine Funktion!
Kartesisches Produkt
Eine Relation ist per Definition eine Teilmenge des Kartesischen Produkts von 2 Mengen zuzüglich einer Regel, z.B. a > 2b.
Aber was ist das kartesische Produkt eigentlich?
Nehmen wir uns zu Anfang erstmal 2 Mengen (A und B):
A = {x,y,z}
B = {1,2,3}
Das kartesische Produkt ist nun eine Menge aus diesen beiden Mengen:
A x B = kartesisches Produkt (das vorne wird "A kreuz B" ausgesprochen)
Diese neue Menge besteht nun jeweils aus Kombinationen aus den Mengen A und B (quasi als würde man 2 Mengen ausmultiplizieren).
A x B = -> Die kleinen a und b sind irgendwelche Elemente in den Mengen A und B.
Wenn man das mit unseren beiden Mengen A und B komplett macht sieht das Ergebnis grafisch ungefähr so aus:

Hierbei ist die Reihenfolge in den jeweiligen "Untermengen" wichtig. Also erst ein Element aus der Menge A, dann eines aus Menge B.
Solche geordneten Mengen nennt man Tupel (vgl. tuples aus z. B. Python).
Damit ist das kartesische Produkt eine Menge aus Tupeln. Es beinhaltet also praktisch alle möglichen Kombinationen aus den Mengen A und B (in dieser Reihenfolge!)
Praxis
Ein praktisches Beispiel für ein kartesisches Produkt ist z. B. ein Skat-Spiel: Jede Karte gibt es in 4 Variationen. Somit wären die Mengen beim Skat:
A (Farben) = {Karo, Herz, Pik, Kreuz}
B (Werte) = {7,8,9,10, Bube, Dame, König, Ass}
Und das kartesische Produkt würde lauten:
A x B = {(Karo,7),(Karo,8)....,(Kreuz,Ass)}
Regeln
Als wichtige Grundregeln gelten somit:
Erstens: Für die Anzahl der Elemente im kartesischen Produkt (zur Erinnerung: dafür stehen die Betragsstriche) gilt bei 2 endlichen Mengen:
|A x B| = |A| * |B|
Zweitens: Da das kartesische Produkt eine Kombination aus 2 Mengen ist, man eine leere Menge aber mit nichts kombinieren kann, gilt:
A x {} = {}
Drittens: Das kartesische Produkt ist nicht-kommutativ. Heißt im Klartext einfach nur, dass die Reihenfolge der Mengen und der Elemente der Tupel wichtig ist:
Praxis
Und wofür betreiben wir jetzt den ganzen Aufwand?
Wenn wir eine Relation oder eine Funktion haben gibt es zusätzlich zu 2 Mengen (Definitions- und Wertebereich) ja immer noch eine Regel (z. B. a > 2b).
Somit inkludiert eine Funktion oder Relation immer nur einen Teil der Tupel aus dem kartesischen Produkt (für die die Regel eben zutrifft).
Eigenschaften von Funktionen
Heißt im Klartext: Werden alle Elemente im Wertebereich W (siehe oben)...
- ...maximal einmal angesprochen (heißt nicht angesprochene Elemente sind völlig okay) -> Injektiv
- ...mindestens einmal angesprochen (die Elemente können auch ruhig öfter angesprochen werden) -> Surjektiv
- ...oder genau einmal angesprochen -> bijektiv
Injektiv
Alle Elemente in W werden maximal einmal angesprochen:

Eine Funktion ist injektiv, wenn:
- Sie streng monoton wachsend/fallend ist, d.h.
- die erste Ableitung > 0 ist
Surjektiv
Alle Elemente in W werden mindestens einmal angesprochen:

Eine Funktion ist surjektiv, wenn:
- Man einen x-Wert des Intervalls in die Funktion einsetzt und der entsprechende y-Wert herauskommt
- Die Funktion stetig ist
Bijektiv
Alle Elemente in W werden genau einmal angesprochen (surjektiv+bijektiv):

Eine Funktion ist bijektiv, wenn:
- Sie sowohl injektiv als auch surjektiv ist.
Praxis
Wenn man die Aufgabe bekommt, eine Funktion auf diese Eigenschaften zu untersuchen sieht das meistens ungefähr so aus:
f: [0,1] -> [0,4], f(x) = x^2
Soll heißen:
[0,1] -> Als erstes kommt der Definitionsbereich D. Bedeutet: Der Bereich der uns auf der x-Achse interessiert.
[0,4] -> Dieser verweist auf den Wertebereich W. Also der Bereich der uns auf der y-Achse interessiert.
f(x) = x^2 -> Am Ende kommt noch die Funktion.
Und wie geht man jetzt vor?
Tipp: Funktion zeichnen!
Dann kann man schon recht genau erkennen, ob und wie oft auf der x-Achse die y-Werte angesprochen werden.
Bei Funktionen mit endlichen Bereichen sollte man zur Kontrolle aber noch die einzelnen Werte im x-Intervall in die Funktion einsetzen, um das Ganze zu überprüfen.
Also:
f(x) = x^2 ist eine simple Parabel. Sie ist damit auf der y-Achse nie negativ.
Das interessiert uns hier aber nicht, wir wollen nur wissen wie sie sich auf der y-Achse von 0 bis 4 verhält. Und zwar nur im Bereich von 0 bis 1 auf der x Achse.
Setzen wir also die x-Werte mal in die Funktion ein:
0^2 = 0
1^2 = 1
Wir sehen: Die y-Werte 0 und 1 werden jeweils einmal angesprochen, die Werte 2, 3 und 4 aber nicht.
Die Funktion ist daher injektiv, aber nicht surjektiv.
Umkehrfunktionen
Siehe Umkehrfunktionen.
Verkettungen
Die Verkettung von 2 Funktionen ist an sich ziemlich simpel:
Man setzt in der ersten Funktion anstelle der Variablen (z. B. x) die komplette andere Funktion ein (wohlgemerkt für jedes x).
Das wird dann "Verkettung der Funktion f(x) mit der Funktion g(x)" gesprochen und ungefähr so geschrieben:
Oder auch so: f(g(x))
Beispielrechnung:
Das gilt übrigens immer, egal wo die Variable steht (z. B. wenn sie als Exponent gesetzt ist).
Einen Fallstrick gibt es aber! Hierzu nochmal ein Beispiel:
Nicht nur, dass hier die Verkettung von g mit f gesucht wird und nicht umgekehrt, es wird zusätzlich nicht mit f(x) verkettet, sondern mit f(2).
Also muss man vor der Verkettung noch 2 in die Funktion f(x) einsetzen und das Ganze dann ausrechnen:
Jetzt kann es an die Verkettung gehen, indem wir das Ergebnis (5) in g(x) einsetzen:
Done:)
Nachschlagewerke
- Was ist eine Funktion - The Simple Club: https://www.youtube.com/watch?v=myLx0d5wmHw
- Das kartesische Produkt - The Simple Club: https://www.youtube.com/watch?v=DrsMLdozJjE
- Relationen und das kartesische Produkt - The Simple Club: https://www.youtube.com/watch?v=rPPUL0KVj2s
- Funktionen advanced - The Simple Club: https://www.youtube.com/watch?v=Jqkja2ODQyI
- Relationen, Kartesisches Produkt, Menge geordneter Paare - Daniel Jung: https://www.youtube.com/watch?v=hYq-d_yP6bo
- Injektiv, Subjektiv, Bijektiv - The Simple Club: https://www.youtube.com/watch?v=xNxuAG9UDN8
- Injektiv, Subjektiv, Bijektiv - Daniel Jung: https://www.youtube.com/watch?v=23jng4oAwI8
- Umkehrfunktionen - Daniel Jung: https://www.youtube.com/watch?v=X8QDtWIWu6Q
- Umkehrfunktionen Voraussetzungen und Berechnung - MathePeter: https://www.youtube.com/watch?v=KiIcbIrmjWg
- Voraussetzungen für Umkehrfunktionen - Daniel Jung: https://www.youtube.com/watch?v=tUUHFqmENvg
- Umkehrfunktionen: Achtung bei x quadrat - Daniel Jung: https://www.youtube.com/watch?v=AszdBZugcdo
- Injektivität beweisen - MathemaTrick: https://www.youtube.com/watch?v=9j6usdTBYbc
- Verkettung von Funktionen 1 -Daniel Jung: https://www.youtube.com/watch?v=y7MmgAdibnY
- Verkettung von Funktionen 2 -Daniel Jung: https://www.youtube.com/watch?v=4pn02EvUZx0
- Verkettung von Funktionen - MathemaTrick: https://www.youtube.com/watch?v=Ln3gAhQfGzI










