Binomialkoeffizienten

Was sind Binomialkoeffizienten?

Vereinfacht gesagt: Mit denen lässt sich berechnen, wie viele Möglichkeiten es gibt aus einer gegebenen Menge von Objekten (nennen wir mal "n") eine gegebene Anzahl von Objekten (nennen wir "k") zu ziehen (ohne zurücklegen).

Sieht dann so aus:

${\binom {n}{k}}$

(Gesprochen: n über k)

Und so wird's berechnet:

${\binom {n}{k}}={\frac {n!}{k!*(n-k)!}}$

Sieht erst mal kompliziert aus, ist es aber gar nicht mal.

Wichtige Regeln

Fangen wir mit dem Wichtigsten an: Welche Gesetze/Regeln gibt es bei der Berechnung und wie erleichtern sie uns das Leben?

Zuerst mal: Eine beliebige Zahl über der 0 oder eine Zahl über sich selbst (meint: n=k) ergibt immer 1:

${\binom {n}{0}}=1$

${\binom {n}{n}}=1$

Eine beliebige Zahl über 1 ergibt immer die Zahl:

${\binom {n}{1}}=n$

Last but not least: Eine beliebige Zahl über 2 stellt die Berechnungsformel etwas um:

${\binom {n}{2}}={\frac {n*(n+1)}{2}}$

Das sind auch schon die Wichtigsten Gesetze zum Binomialkoeffizienten.

Allgemeines

Hat man eine beliebige Aufgabe zum Binomialkoeffizienten gilt es erstmal die Formel von oben anzuwenden:

${\binom {49}{6}}={\frac {49!}{6!*(49-6)!}}={\frac {49!}{6!*43!}}$

Es wäre jetzt natürlich völlig hirnrissig die Fakultäten aufzulösen und drauflos zu rechnen. Aber die Formel ist so gestaltet, dass man angenehm leicht kürzen kann.

Wenden wir doch erst mal ein paar Fakultätsregeln an:

$={\frac {49*48*47*46*45*44*43!}{6!*43!}}={\frac {49*48*47*46*45*44}{6*5*4*3*2*1}}$

Jetzt können wir sogar noch weiter kürzen:

Wir kürzen 45 mit 5 und die resultierende 9 im Zähler mit 3 zu 3;

Wir kürzen 48 mit 6 und die resultierende 8 im Zähler mit 4 zu 2;

und wir kürzen 44 mit 4 zu 11.

Das ergibt dann:

$={\frac {49*2*47*46*3*11}{1}}=49*2*47*46*3*11$

Das ergibt dann:

$=13.986.816$

Aufgabe gelöst:) Und was lernen wir daraus: Kein Lotto spielen!

Binomialkoeffizienten und das Pascalsche Dreieck

Kurze Erinnerung an meine erste GFS: Das Pascalsche Dreieck ist ein wortwörtliches Dreieck, das nur aus Einsen an der Spitze und an den Rändern besteht. In der Mitte stehen immer die Ergebnisse der Additionen der beiden schräg darüber liegenden Zahl:

(Ich habe jetzt wirklich keine Lust das Dreieck im Wiki-Syntax hier hinzumalen. Ein Screenshot tuts auch.)

Das Pascalsche Dreieck.

Und wie soll das jetzt für Binomialkoeffizienten taugen? Nun, betrachten wir das Dreieck doch mal etwas genauer.

Oder besser gesagt: geben wir seinen Zeilen und Spalten Nummern. Wichtig: Wir fangen bei 0 an zu zählen!:

Das Pascalsche Dreieck nummeriert.

Jetzt können wir die Binomialkoeffizienten wie eine Art "Landkarte" benutzen:

Haben wir beispielsweise den Koeffizienten ${\binom {5}{3}}$ wird er mit der gelernten Formel ja folgendermaßen gelöst:

$={\frac {5*4*3*2*1}{(3*2*1)*(2*1)}}={\frac {5*4}{2*1}}={\frac {20}{2}}=10$

Nutzen wir jedoch das Pascalsche Dreieck navigieren wir einfach 5 Schritte nach unten und 3 nach rechts (zzgl. jeweils der 0). Wir landen beim korrekten Ergebnis: 10.

Hat man das Dreieck also in ausreichender Größe vorliegen kann man die Ergebnisse von Koeffizienten-Rechnungen recht einfach ablesen:

Navigation im Dreieck anhand von mehreren Beispielen.

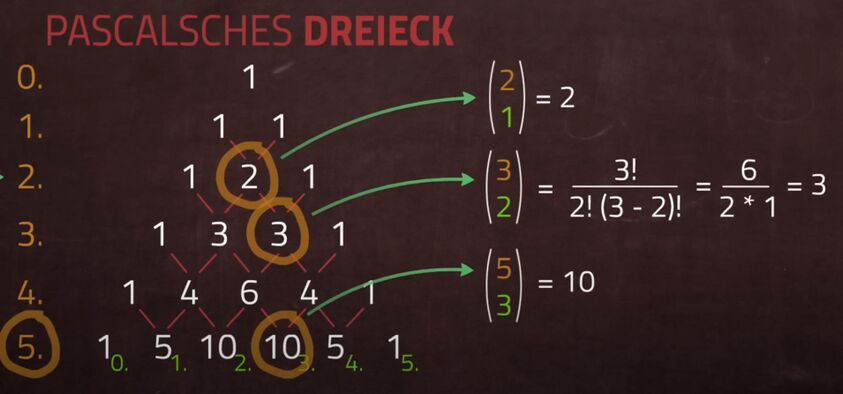
q.e.d. :D

Beispielaufgaben

Erste Aufgabe

${\binom {15}{3}}$

Zweite Aufgabe

${\binom {20}{19}}+{\binom {25}{2}}$

Dritte Aufgabe

${\frac {\binom {40}{20}}{\binom {39}{19}}}$

Nachschlagewerke

• Binomialkoeffizient - The Simple Club: https://www.youtube.com/watch?v=QAaeSC3hItw
• Binomialkoeffizient mit dem Pascalschen Dreieck - The Simple Club: https://www.youtube.com/watch?v=QQa2aoTD3d0
• Hohe Potenzen auflösen - The Simple Club: https://www.youtube.com/watch?v=WXtO2S_mq80